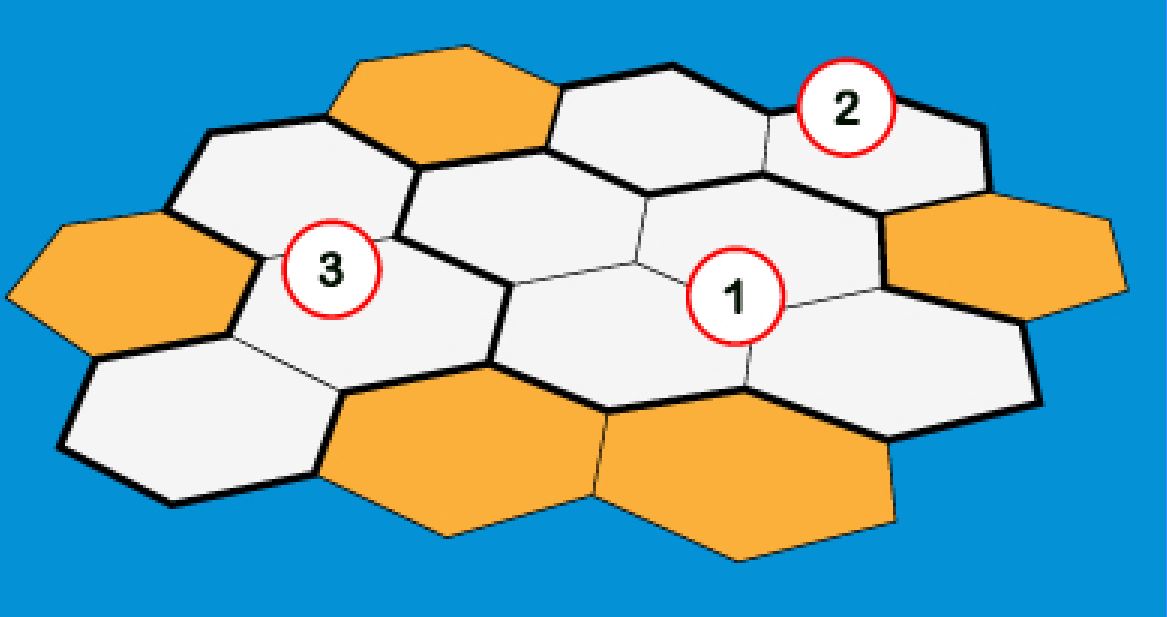
1)
Източник: Cernecka Natalja / Shutterstock
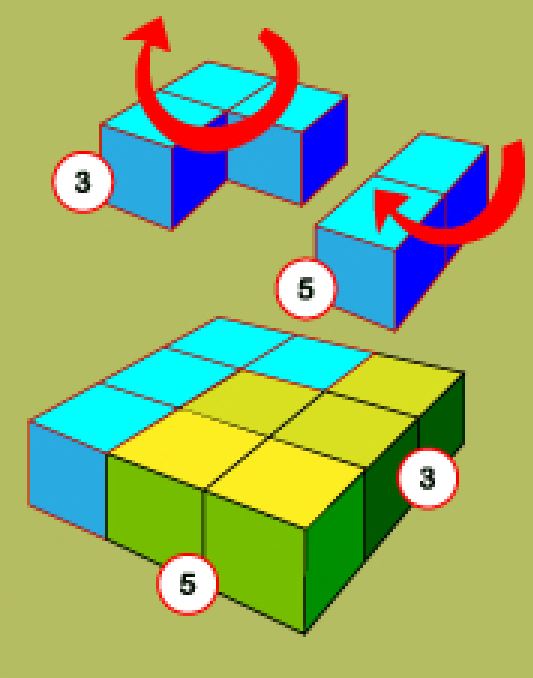
2) Номер 5
3) Очевидно е, че в случая трябва да мислите нестандартно, тъй като е невъзможно да разпределите 10 монети в 3 чаши и във всяка чаша да има нечетен брой. Едно потенциално решение е да поставите 3 монети в първата чаша, 2 във втората и 5 в третата, след което да сложите втората чаша в първата. Така ще има нечетен брой монети във всяка една от чашите.
4) Да разгледаме потенциалните варианти.
Ако имам >=5 монети (т.е. 5, 6, 7 и т.н.), то твърдения 1 и 3 са верни. Но ние знаем, че само едно твърдение може да е вярно. Т.е. >=5 не е валиден вариант.
Ако имам 4, 3 или 2 монети, то твърдения 1 и 2 са верни. Т.е. и този случай не е валиден.
А ако имам 1 монета? Дори и в този случай твърдения 1 и 2 ще са верни. Пак не става.
Какво остава тогава? 0. При нула монети единственото вярно твърдение е <5 монети.
5) Това са огледални числа, което означава, че следващият символ е:
6) От първото състезание можем да заключим, че Алис е по-бърза от Боб и че когато Алис избягва 100 метра, Боб избягва 90.
Във второто състезание, когато Алис достигне 90-ия метър, тя реално е бягала 100 метра, защото е започнала с 10 метра зад стартовата линия. От първото състезание знаем, че когато Алис избягва 100 метра, Боб изминава 90. Това означава, че по време на второто състезание на 90-ия метър ще са наравно. И двамата трябва да избягат 10 метра, за да достигнат финала. Ние обаче знаем, че принципно Алис е по-бързата. Т.е. и в сегашния случай тя ще спечели.
7) Днес е 11-ият ѝ рожден ден.
8)
Източник: Cernecka Natalja / Shutterstock
9)
Източник: Cernecka Natalja / Shutterstock
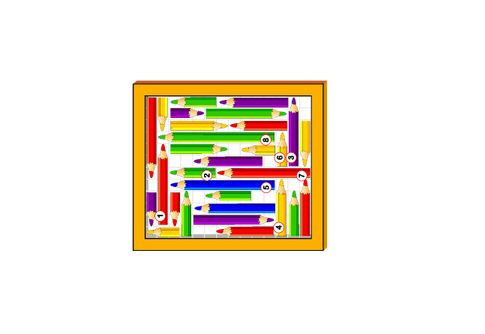
10) Номер 8.
11)
Източник: Cernecka Natalja / Shutterstock
12. В
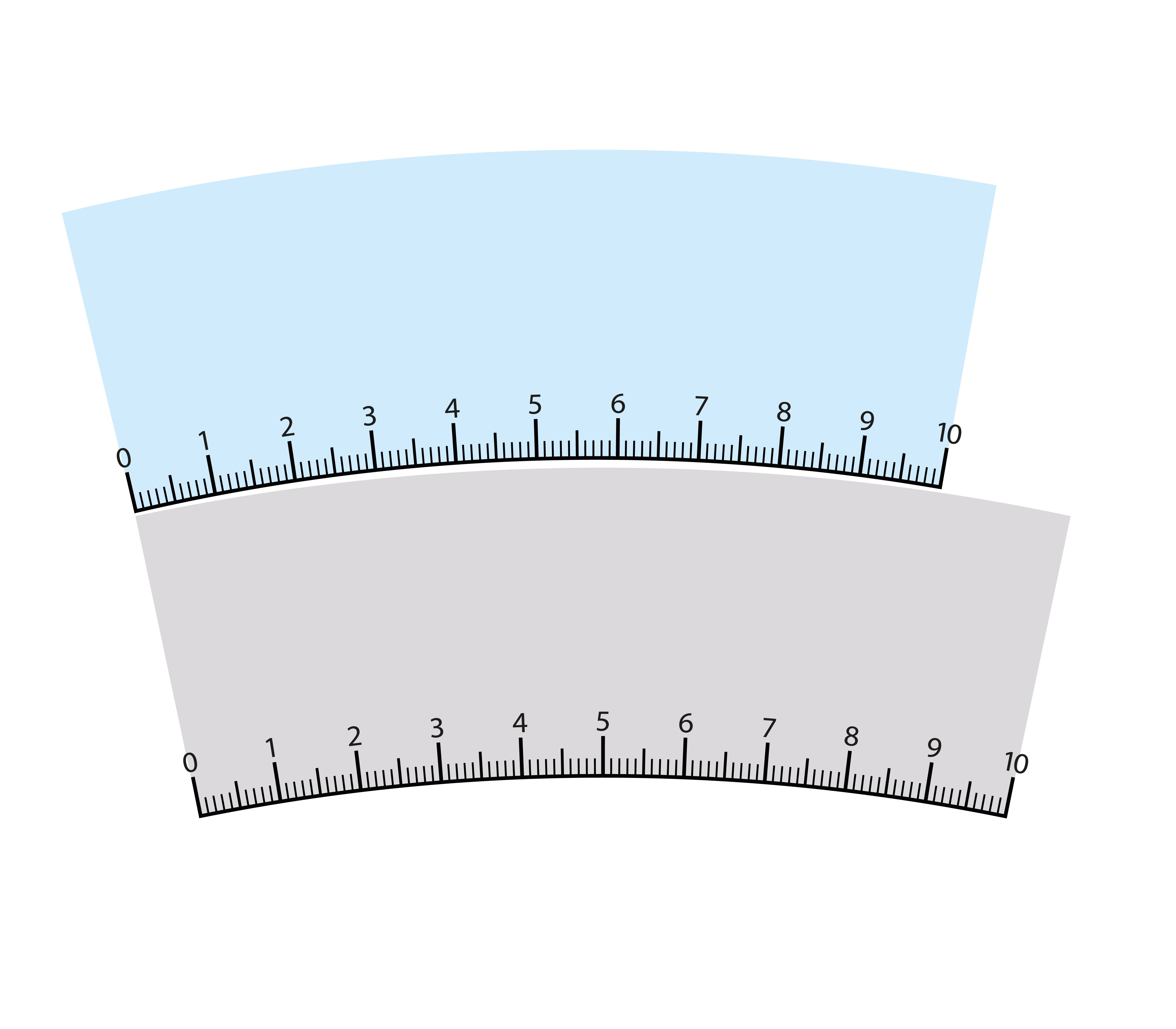
13. Еднакви са.
Източник: Peter Hermes Furian / Shutterstock
