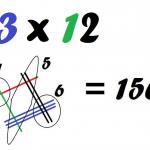Съставните блокове на числата
За да продължим темата за умножението, трябва да извършим и малко деление. Помнете - делението разделя числата на парчета с равни размери.
12 делено на 3 е 4.
Това означава, че 12 може да бъде разделено на 3 части, всяка от които е с размер 4.
3 и 4 са цели числа. Съответно те са множителите на 12, а 12 може да се раздели на 3 и 4. Ако едно число се дели единствено на себе си или на 1, то това означава, че то е просто.
Съществуват обаче най-различни начини да изпишем 12 като продукт на 2 числа.
12 × 1
6 × 2
4 × 3
3 × 4
2 × 6
1 × 12
Нещо повече - можем да видим това, ако погледнем таблицата за умножение:
Броят на оцветените квадратчета в таблицата по-горе показва, че съществуват 6 начина, по които можете да направите правоъгълник с площ 12 с цели числа. Това е броят на различните начини, по които имате възможност да изпишете 12 като продукт на 2 числа.
Може би сте забелязали, че оцветените квадратчета образуват гладка извивка - наистина е така! Тази извивка, съединяваща квадратчетата, е известна като хипербола и се получава с уравнението a x b = 12, при което не е задължително a и b да са цели числа.
Нека да погледнем отново към списъка с числа, които дават 12. Можем допълнително да факторизираме всяко едно от числата, които дават 12 (с изключение на 1 и простите). Например:
12 = 6 × 2 = (2 × 3) × 2
12 = 4 × 3 = (2 × 2) × 3
Без значение как точно ще го направим, докато факторизираме числата така, че да останат единствено прости, винаги получаваме две 2 и една 3.
Този продукт:
2 x 2 x 3
представлява декомпозиция на 12 на прости числа. Резултатът е уникален за това число. Има само един начин, по който можете да изпишете едно число като продукт от прости числа. И всеки продукт от прости дава различно число. В математиката това се нарича Фундаменталната теорема на аритметиката.
Тази декомпозиция ни позволява да научим някои важни неща за числата.
Така например от 12 = 2 x 2 x 3 разбираме на мига, че 12 се дели само на 2 и 3 (на други прости числа като 5 и 7 - не).
