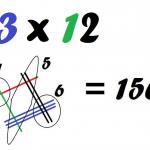Освен това всяко число, умножено по 12, също ще се дели на същите числа. Например 11 x 12 = 132. Резултатът също се дели на 1, 2, 3, 4, 6 и 12, подобно на 12. Ако умножим всяко едно от тях с 11, откриваме, че 132 се дели също така на 11, 12, 33, 44, 66 и 132.
Тази проста декомпозиция прави умножението доста по-лесно. Ако не знаете колко е 11 x 12, то достатъчно е да сте наясно, че 12 = 2 x 2 x 3. Впоследствие можете да достигнете до резултата стъпка по стъпка:
11 x 12
= 11 x 2 × 2 × 3
= ((11 x 2) × 2) × 3
= (22 × 2) × 3
= 44 × 3
= 132
Ако простите числа от декомпозицията са достатъчно малки (например 2, 3 или 5), то умножението става наистина лесно и приятно. По този начин, когато умножавате по 4 (= 2 x 2), 6 (= 2 x 3), 8 (= 2 x 2 x 2) или 9 (= 3 x 3), вече няма да се затруднявате толкова много.
Така например ако не можете да запомните колко е 9 по дадено число, това не е проблем, стига да можете да умножавате по 3 два пъти. Този метод обаче не помага в случаите, когато трябва да умножавате големи прости числа (Как става това с 11? Вижте следното видео).
И така - разбиването на числата на техните просто множители може да направи сложното умножение доста по-лесно. Трикът работи дори и с по-големи числа.
Т. напр. декомпозиция на 756 е 2 x 2 x 3 x 3 x 3 x 7. Съответно когато умножавате по 756, е достатъчно да умножите другото число по тези малки числа. Разбира се, откриването на простите множители на големите числа обикновено е трудна задача. Затова този трик е полезен в случаите, когато вече ги знаете.
Не на последно място - декомпозицията на прости числа ни дава фундаментални знания за числата. Тази информация е особено полезна както в математиката, така и в други сфери, като криптографията и интернет сигурността.
